Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Рассмотрим каждое утверждение:
1) "Существует ромб, который не является квадратом".
Ромб будет
квадратом только в одном случае - если все углы ромба будут равны 90°. При других значениях углов ромб не будет квадратом. Следовательно, это утверждение верно.
2) "Если две стороны треугольника равны, то равны и противолежащие им углы", это утверждение верно, т.к. это утверждение соответствует
свойству
равнобедренного треугольника.
3) "Касательная к окружности параллельна радиусу, проведённому в точку касания", это утверждение неверно, т.к. противоречит
свойству
касательной.
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=11, CK=20.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
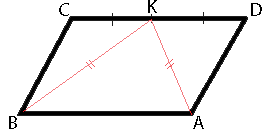В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
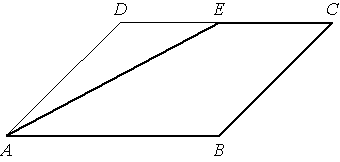Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-02-16 22:19:41) Левиза: Угол K трапеция KLMN с основаниями LM и KN,вписанной в окружность,равен 76 градусов.Найдите угол M этой трапеции.Ответ дайте в градусах.
(2022-02-16 22:16:26) : Угол K трапеция KLMN с основаниями LM и KN,вписанной в окружность,равен 76 градусов.Найдите угол M этой трапеции.Ответ дайте в градусах
(2022-02-16 22:12:43) : в треугольнике ABC изветно,что угол BAC=84градусов,AD-бессектриса.Найдите угол BAD.Ответ дайте в градусах