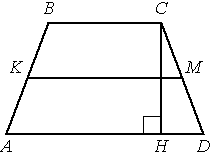
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
Средняя линия трапеции Lср=(AD+BC)/2, отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
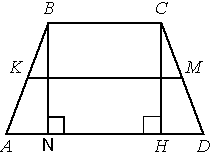и рассмотрим треугольники CDH и ABN. AB=CD (по условию задачи), BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним. Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD, AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*16-4=28, тогда HD=(28-4)/2=12.
Ответ: HD=12.
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
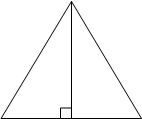Высота равностороннего треугольника равна
15√
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
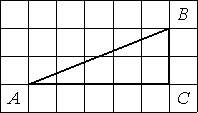Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: