Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgABC=AC/CB=2,4 => CB=AC/2,4.
По
теореме Пифагора AB2=AC2+CB2
AB2=AC2+(AC/2,4)2
AB2=6,76*AC2/5,76
AB=2,6*AC/2,4=1,3*AC/1,2
Необходимо вычислить AC.
По
теореме о сумме углов треугольника для треугольника ABC:
/CAB=180°-90°-/ABC
Для треугольника ACP:
/CAB=180°-90°-/ACP
Следовательно, /ABC=/ACP.
Рассмотрим треугольник ACP.
По
определению tgACP=AP/CP=2,4 => AP=2,4*CP.
По
теореме Пифагора AC2=CP2+AP2
AC2=CP2+(2,4*CP)2
AC2=6,76*CP2
AC=2,6*CP
CP=AC/2,6
r=(AP+CP-AC)/2
2*r=2,4*CP+CP-AC
2*r=3,4CP-AC
2*12=3,4*AC/2,6-AC
24=0,8*AC/2,6
30=AC/2,6
78=AC
Вычислив AC, мы можем вычислить AB и CP, указанные выше:
AB=1,3*AC/1,2=1,3*78/1,2=13*78/12=13*26/4=84,5
CB=AC/2,4=78/2,4=32,5
R=(AC+CB-AB)/2, тогда получаем:
R=(78+32,5-84,5)/2=13.
Ответ: R=13.
Поделитесь решением
Присоединяйтесь к нам...
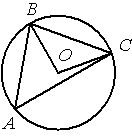Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: