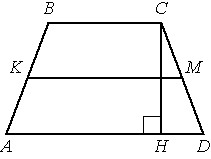
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
Средняя линия трапеции Lср=(AD+BC)/2, отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
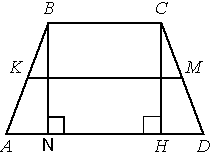и рассмотрим треугольники CDH и ABN. AB=CD (по условию задачи), BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним. Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD, AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*12-4=20, тогда HD=(20-4)/2=8.
Ответ: HD=8.
Поделитесь решением
Присоединяйтесь к нам...
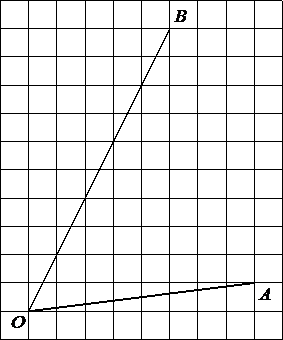Найдите тангенс угла
AOB.
Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
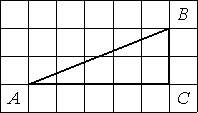Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: