В треугольнике ABC угол C прямой, AC=4, cosA=0,8. Найдите AB.
По
определению косинуса cosA=AC/AB => AB=AC/cosA=4/0,8=5.
Ответ: AB=5.
Поделитесь решением
Присоединяйтесь к нам...
У треугольника со сторонами 4 и 16 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне?
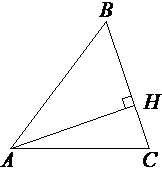В остроугольном треугольнике ABC высота AH равна 20√
Сторона равностороннего треугольника равна 12√3. Найдите радиус окружности, описанной около этого треугольника.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
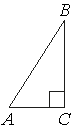В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-10-13 00:42:51) : Суммадвух углов равнобедренной трапеции равна 34 градусов. Найдите больший угол трапеции
(2015-05-16 10:04:21) илгиз исхакоич: ппррнп