Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Угол ∠BCA=∠CAD, т.к. это
внутренние накрест-лежащие углы.
Следовательно, ∠BCD=80°+30°=110°.
По
свойству равнобедренной трапеции ∠BCD=∠ABC=110°.
Ответ: ∠ABC=110°
Поделитесь решением
Присоединяйтесь к нам...
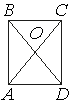Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-10-04 12:42:21) Администратор: Потому, что AB не параллельна CD.
(2021-09-30 09:52:25) : а почему угла BAC и ACD не являются накрест лежащими?