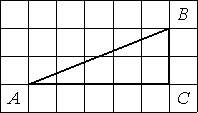
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
По
определению тангенса: tgB=AC/CB=5/2=2,5.
Ответ: tgB=2,5.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна
180°, то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: