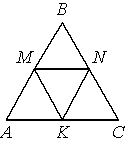
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
По условию задачи AB=BC=CA (т.к. треугольник ABC -
равносторонний). Значит AK=KC=CN=NB=BM=MA.
Тогда, MN -
средняя линия треугольника ABC. Следовательно, MN=AK и MN||AK (по
теореме о средней линии).
NK - тоже
средняя линия, равна AM и параллельна AM.
Получается, что AM=MN=NK=KA, т.е. AMNK -
ромб (по
свойству ромба).
Поделитесь решением
Присоединяйтесь к нам...
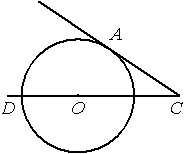Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
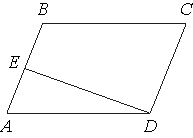Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
В треугольнике ABC угол C равен 90°, BC=5, AC=2.
Найдите tgB.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=36, BC=42 и CD=24.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: