
Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Рассмотрим каждое утверждение:
1) "Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника".
Высота, проведенная к основанию является и
медианой, и биссектрисой (по
свойству равнобедренного треугольника), т.е. является
серединным перпендикуляром. А центром описанной окружности является точка пересечения
серединных перпендикуляров (
теорема об описанной окружности). Следовательно, это утверждение верно.
2) "Квадрат является прямоугольником", это утверждение верно (по
определению).
3) "Сумма углов любого треугольника равна 180°", это утверждение верно (по
теореме).
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и ADB подобны.
Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD=16. Докажите, что треугольники CBD и ADB подобны.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
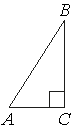 В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
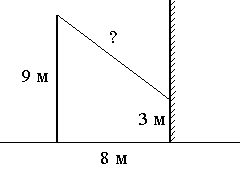 От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Комментарии: