
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
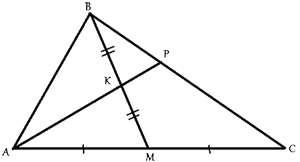 По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
SABM=SBCM=(SABC)/2.
В свою очередь, AK является медианой для треугольника АВМ, следовательно, по тому же
свойству медианы
SABК=SAKM=(SABM)/2=(SABC)/4.
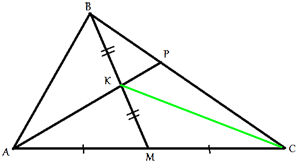 Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
SCMK=SCKB=(SCMB)/2=(SABC)/4.
Проведем отрезок МЕ, параллельно АР.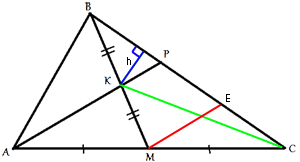 МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
Проведем
высоту h, как показано на рисунке. h является общей высотой для треугольников СКВ и СКР.
Выше мы определили, что SCKB=(SABC)/4. Площадь этого же треугольника =(1/2)*h*BC.
SCKP=(1/2)*h*РС=(1/2)*h*(2/3)*ВС=(2/3)*(1/2)*h*BC=(2/3)SCKB=(2/12)SABC
=(1/6)SABC.
SKPCM=SCMK+SCKP=(SABC)/4+(1/6)SABC=(5/12)SABC.
Следовательно отношение SABK к SKPCM равно ((1/4)SABC)/((5/12)SABC)=3/5=0,6.
Ответ: SABK/SKPCM=3/5=0,6.
Поделитесь решением
Присоединяйтесь к нам...
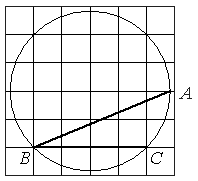 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30Х40Х50 (см) можно поместить в кузов машины размером 3Х2Х3,5 (м)?
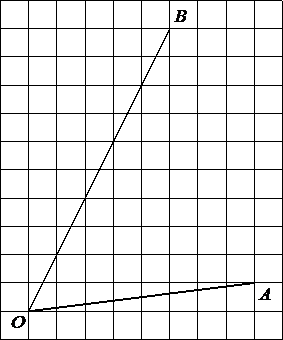 Найдите тангенс угла
AOB.
Найдите тангенс угла
AOB.
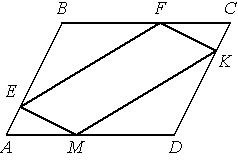 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
 Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Комментарии:
(2016-04-24 16:09:22) Администратор: Наталья, спасибо за предложение. Принцип Вы использовали тот же самый, только сократили запись. Для пользователей сайта некоторые моменты могут оказаться непонятными. Например вот этот: S2+S3=2x/3, т.к. PC=(2/3)BC. Но спасибо за проявленную инициативу.
(2016-04-22 02:12:00) Наталья: Предлагаю немножко упростить, оставить только ME//AP. EC=PE, т.к. ME-средняя линия APC. PE=BP, т.к. KP-средняя линия MBE. EC=PE=PB. Обозначим: S1 - площадь ABK, S2 - площадь AKM, S3 - площадь KPCM, х - площадь ABC. S1=S2=x/4 S2+S3=2x/3, т.к. PC=2/3BC S3=2x/3-x/4=5x/12 S1/S3=(x/4):(5x/12)=3/5