
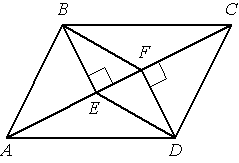
 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
1) Рассмотрим треугольники ABE и CDF.
AB=CD (по
свойству параллелограмма).
/BAE=/DCF (т.к. это
внутренние накрест-лежащие углы для параллельных BC и AD и секущей AC).
/BEA=/DFC (т.к. оба эти угла прямые по условию).
Если два угла у данных треугольников попарно равны, то и третьи углы равны (по
теореме о сумме углов треугольника).
Следовательно треугольники ABE и CDF равны (по
второму признаку равенства треугольников). Отсюда следует, что BE=FD
2) Рассмотрим треугольники BFE и DEF.
BE=FD (из пункта 1), EF-общая сторона, /BEF=/DFE (т.к. это прямые углы по условию).
Следовательно треугольники BFE и DEF равны (по
первому признаку равенства треугольников). Отсюда следует, что BF=ED.
3) В итоге получаем, BF=ED и BE=FD, следовательно ВFDЕ —
параллелограмм (по
свойству параллелограмма).
Следовательно, ВF и DЕ параллельны (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
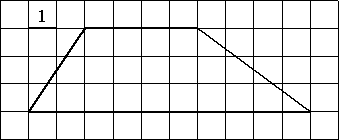 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=40, BC=45 и CD=24.
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Комментарии: