Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ (по свойству равнобедренного треугольника). По теореме о сумме углов треугольника 180°=/AOB+/ОАВ+/ОBA. => /ОАВ+/ОBA=180°-60°=120°
А т.к. /ОАВ=/ОBA, то /ОАВ=/ОBA=120°/2=60°
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, R=ОВ=ОА=АВ=3.
Ответ: R=3.
Поделитесь решением
Присоединяйтесь к нам...
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
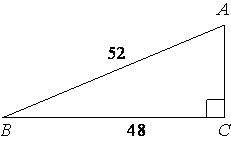Найдите площадь треугольника, изображённого на рисунке.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет из бруса длиной 80 дм, имеющего в сечении прямоугольник размером 30 см на 40 см?
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-04-30 20:17:06) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-04-30 16:04:19) : на окружности по разные стороны от диматера AB взяты точки M и N