
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ = 60° (по свойству равнобедренного треугольника). Заметим, что /АОВ тоже равен 60° (по теореме о сумме углов треугольника). 180°-60°-60°=60°.
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=7.
Ответ: АВ=7.
Поделитесь решением
Присоединяйтесь к нам...
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 11°?
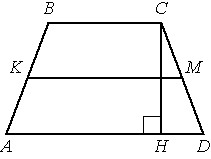 В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
 На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?
Комментарии: