
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи BD=BE, следовательно треугольник BDE - равнобедренный (по
определению). По
свойству равнобедренного треугольника /BDE=/BED.
Смежные им углы тоже равны, /BDA=/BEC.
2) Рассмотрим треугольники ABD и CBE.
AD=CE (по условию),
BD=BE (По условию),
/BDA=/BEC (из п.1),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
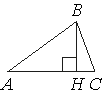 В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
 Площадь ромба равна 30, а периметр равен 24. Найдите высоту ромба.
Площадь ромба равна 30, а периметр равен 24. Найдите высоту ромба.
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Комментарии: