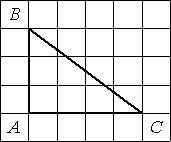
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
По
определению, tgC=AB/AC=3/4=0,75.
Ответ: tgC=0,75.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
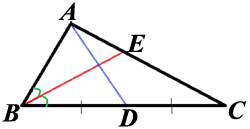В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
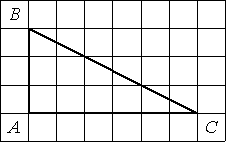Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Синус острого угла A треугольника ABC равен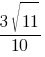 
. Найдите CosA.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: