
 В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
NK - является
средней линией треугольника ABC и равна половине AB.
MK - является
средней линией треугольника ABC и равна половине BC.
Т.к. AB=BC (по условию), то NK=MK.
Следовательно треугольник MNK -
равнобедренный.
Поделитесь решением
Присоединяйтесь к нам...
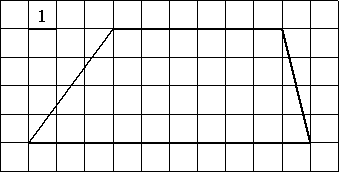 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
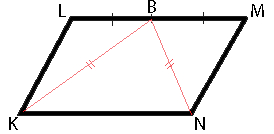 В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
 Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Комментарии: