
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ (по свойству равнобедренного треугольника).
По теореме о сумме углов треугольника можем записать:
180°=/AOB+/OBA+/BAO
180°=60°+/OBA+/BAO
120°=/OBA+/BAO
А так как /OBA=/BAO, то /OBA=/BAO=120°/2=60°.
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=4.
Ответ: АВ=4.
Поделитесь решением
Присоединяйтесь к нам...
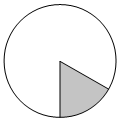 Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Площадь круга равна 90. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
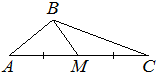 В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
 На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Комментарии: