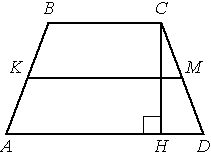
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
Средняя линия трапеции Lср=(AD+BC)/2
Отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
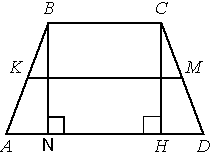и рассмотрим треугольники CDH и ABN.
AB=CD (по условию задачи)
BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним.
Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD
AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда:
AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*16-6=26, тогда:
HD=(26-6)/2=10.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
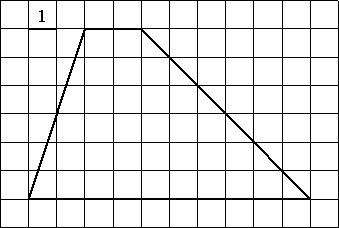Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
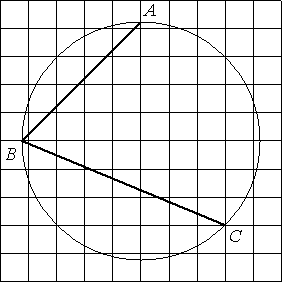В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-01-19 20:09:01) Администратор: Вам что-то не нравится?
(2018-01-19 12:49:04) : это фуфло