Средний рост девочек класса, где учится Таня, равен 164 см. Рост Тани 162 см. Какое из следующих утверждений верно?
1) В классе обязательно есть девочка ростом 164 см.
2) В классе обязательно есть девочка ростом менее 162 см.
3) В классе обязательно есть девочка ростом более 164 см.
4) В классе обязательно есть хотя бы 2 девочки ростом более 164 см.
Рассмотрим каждое утверждение:
1) "В классе обязательно есть девочка ростом 164 см." Рассмотрим такой вариант: ровно половина девочек в классе, включая Таню, ростом 162 см, другая половина - ростом 166 см. Все условия задачи выполняются, а утверждение неверно.
2) "В классе обязательно есть девочка ростом менее 162 см." - это утверждение так же неверно, см. пример из п.1).
3) "В классе обязательно есть девочка ростом более 164 см." - это утверждение верно. Если есть девочка, рост которой ниже среднего значения, то есть и девочка, рост которой выше среднего значения.
4) "В классе обязательно есть хотя бы 2 девочки ростом более 164 см." - это утверждение неверно. Если рассмотреть пример из п.1) с оговоркой, что в классе только две девочки. Т.е. Таня ростом 162 см. и другая девочка ростом 166.
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
На диаграмме показан возрастной состав населения Китая. Определите
по диаграмме, какая из возрастных категорий самая малочисленная.
1) 0–14 лет
2) 15–50 лет
3) 51–64 лет
4) 65 лет и более
В ответе запишите номер выбранного варианта ответа.
На тарелке лежат одинаковые на вид пирожки: 3 с капустой, 8 с рисом и 1 с луком и яйцом. Игорь наугад выбирает один пирожок. Найдите вероятность того, что он окажется с капустой.
На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каких продуктах содержание углеводов превышает 50%.
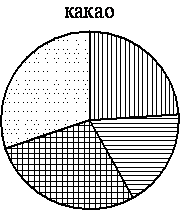
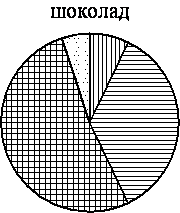
*К прочему относятся вода, витамины и минеральные вещества.
1) какао
2) шоколад
3) фасоль
4) грибы
В фирме такси в данный момент свободно 20 машин: 2 чёрных, 2 жёлтых и 16 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: