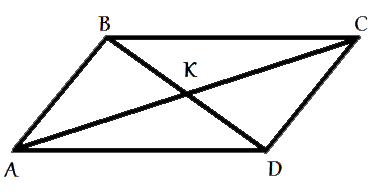
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BKC.
Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников, AB=CD и BC=AD (по
свойству параллелограмма), следовательно рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACB, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок BK - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь BKC равна половине площади треугольника ACB. SBKC=SACB/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: