В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BKC.
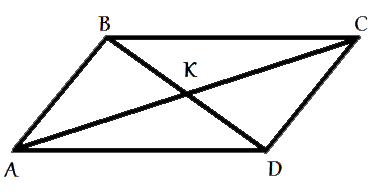Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников, AB=CD и BC=AD (по
свойству параллелограмма), следовательно рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACB, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок BK - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь BKC равна половине площади треугольника ACB. SBKC=SACB/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinA=0,75, AC=√
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
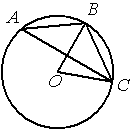Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: