
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Рассмотрим каждое утверждение.
1) "Через две различные точки на плоскости проходит единственная прямая", это утверждение верно (
свойство прямой).
2) "Центром вписанной в треугольник окружности является точка пересечения его биссектрис", это утверждение верно (
свойство вписанной окружности).
3) "Если гипотенуза и острый угол одного
прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны". Прилежащий к известному острому углу катет равен проиведению косинуса этого угла на гипотенузу (из
определения косинуса). Следовательно этот катет тоже будет равен у обоих треугольников. Тогда по
первому признаку равенства, получается, что эти треугольники равны. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
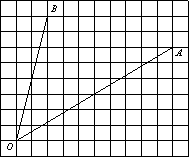 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
 Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 36, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
 Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
Основания трапеции равны 11 и 19, а высота равна 9. Найдите среднюю линию этой трапеции.
 Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Комментарии: