Косинус острого угла A треугольника ABC равен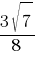 
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
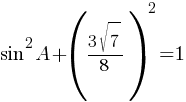
По второму правилу действий со степенями:
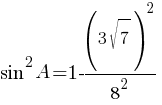
По первому правилу действий со степенями:
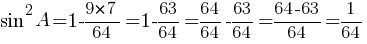
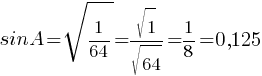(использовали второе свойство арифметического корня)
Ответ: 0,125
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
Какое из следующих утверждений верно?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: