
Синус острого угла A треугольника ABC равен 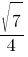 . Найдите CosA.
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться основной тригонометрической формулой:
sin2A+cos2A=1
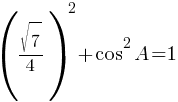
По второму правилу действий со степенями:
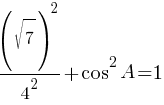
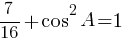
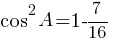
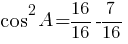
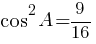
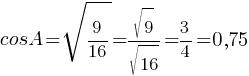
Ответ: 0,75
Поделитесь решением
Присоединяйтесь к нам...
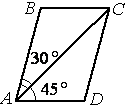 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
 Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
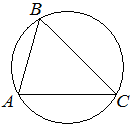 В треугольнике ABC угол C равен 45°, AB=6√
В треугольнике ABC угол C равен 45°, AB=6√
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Комментарии: