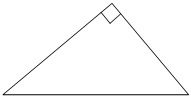
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Обозначим длину гипотенузы как "х".
По
теореме Пифагора:
x2=302+402
x2=900+1600
x2=2500
x=√2500=50
Ответ: 50
Поделитесь решением
Присоединяйтесь к нам...
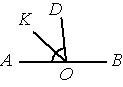Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
Сторона AB параллелограмма ABCD вдвое больше стороны AD.
Точка L — середина стороны AB. Докажите, что DL — биссектриса
угла ADC.
Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: