Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
По
первому свойству квадрата, все его углы прямые, следовательно, треугольники, которые образует диагональ, прямоугольные.
Т.е. к этим треугольникам можно применить теорему Пифагора.
По определению квадрата, все его стороны равны, следовательно катеты этих треугольников равны:
d2=(9√2)2+(9√2)2
d2=2(9√2)2
По первому правилу действий со степенями:
d2=2*92(√2)2
d2=2*81*2=324
d=√324=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
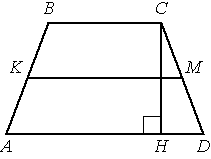В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: