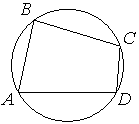
Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
По 3-му свойству описанной окружности:
∠A+∠C=180°
∠C=180°-∠A=180°-82°=98°
Ответ: 98
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Косинус острого угла A треугольника ABC равен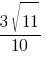 
. Найдите sinA.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: