
 Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=7, CP=14, DP=10. Найдите AP.
По
пятому свойству хорды:
AP*CP=DP*BP
AP*14=10*7 |:7
AP*2=10 |:2
AP=5
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
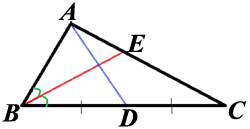 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
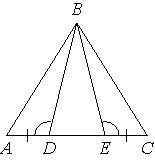 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
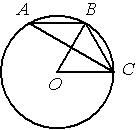 Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=60° (см. рисунок). Найдите величину угла BAC (в градусах).
Комментарии: