Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 20 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 210 км, скорость первого велосипедиста равна 20 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Обозначим:
S1 - путь, который проехал первый велосипедист.
S2 - путь, который проехал второй велосипедист.
t1 - время в пути первого велосипедиста.
t2 - время в пути второго велосипедиста.
S1+S2=210 км.
Первый велосипедист ехал на 20 минут меньше второго, т.к. сделал остановку.
20 минут = 1/3 часа.
t2=t1+1/3
Получается:
S1=20*t1
S2=20*t2
20*t1+30*t2=210
20t1+30(t1+1/3)=210
20t1+30t1+30*1/3=210
50t1+30/3=210
50t1+10=210
50t1=210-10=200
t1=200/50=4
S1=20*t1=20*4=80
S1+S2=210
S2=210-S1=210-80=130
Ответ: 130
Поделитесь решением
Присоединяйтесь к нам...
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно через 6 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч?
О числах a и c известно, что a<c. Какое из следующих неравенств неверно
1) a+8<c+8
2) -a/33<-c/33
3) a-2<c-2
4) -a/33<c/33
Укажите решение неравенства 4x+5≥6x-2.
1) 
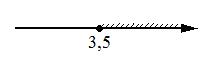
2) 
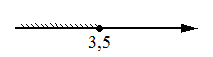
3) 
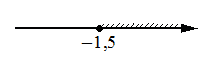
4) 
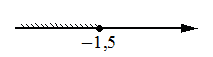
Решите уравнение 3x+5+(x+5)=(1-x)+4.
Решите уравнение (x2-9)2+(x2-2x-15)2=0.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: