Косинус острого угла A треугольника ABC равен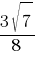 
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
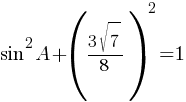
По второму правилу действий со степенями:
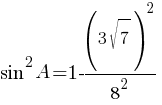
По первому правилу действий со степенями:
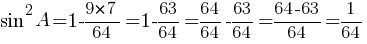
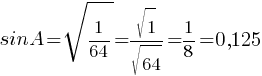(использовали второе свойство арифметического корня)
Ответ: 0,125
Поделитесь решением
Присоединяйтесь к нам...
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
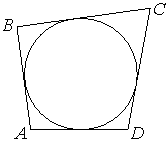Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Найдите угол ABC. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Треугольник со сторонами 1, 2, 4 не существует.
3) Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Хочу получать новые решения
Ни какого спама
Автор: Таська
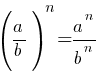
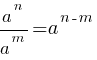
Комментарии: