
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ950 –Є–Ј 1087 |
–Ш–Љ–µ—О—В—Б—П –і–≤–∞ —Б–Њ—Б—Г–і–∞, —Б–Њ–і–µ—А–ґ–∞—Й–Є–µ 12 –Ї–≥ –Є 8 –Ї–≥ —А–∞—Б—В–≤–Њ—А–∞ –Ї–Є—Б–ї–Њ—В—Л —А–∞–Ј–ї–Є—З–љ–Њ–є –Ї–Њ–љ—Ж–µ–љ—В—А–∞—Ж–Є–Є. –Х—Б–ї–Є –Є—Е —Б–ї–Є—В—М –≤–Љ–µ—Б—В–µ, —В–Њ –њ–Њ–ї—Г—З–Є–Љ —А–∞—Б—В–≤–Њ—А, —Б–Њ–і–µ—А–ґ–∞—Й–Є–є 65% –Ї–Є—Б–ї–Њ—В—Л. –Х—Б–ї–Є –ґ–µ —Б–ї–Є—В—М —А–∞–≤–љ—Л–µ –Љ–∞—Б—Б—Л —Н—В–Є—Е —А–∞—Б—В–≤–Њ—А–Њ–≤, —В–Њ –њ–Њ–ї—Г—З–µ–љ–љ—Л–є —А–∞—Б—В–≤–Њ—А –±—Г–і–µ—В —Б–Њ–і–µ—А–ґ–∞—В—М 60% –Ї–Є—Б–ї–Њ—В—Л. –°–Ї–Њ–ї—М–Ї–Њ –Ї–Є–ї–Њ–≥—А–∞–Љ–Љ–Њ–≤ –Ї–Є—Б–ї–Њ—В—Л —Б–Њ–і–µ—А–ґ–Є—В—Б—П –≤–Њ –≤—В–Њ—А–Њ–Љ —А–∞—Б—В–≤–Њ—А–µ?
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ –Ї–∞–Ї "—Е" –њ—А–Њ—Ж–µ–љ—В–љ–Њ–µ —Б–Њ–і–µ—А–ґ–∞–љ–Є–µ –Ї–Є—Б–ї–Њ—В—Л –≤ –њ–µ—А–≤–Њ–Љ —А–∞—Б—В–≤–Њ—А–µ.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ –Ї–∞–Ї "y" –њ—А–Њ—Ж–µ–љ—В–љ–Њ–µ —Б–Њ–і–µ—А–ґ–∞–љ–Є–µ –Ї–Є—Б–ї–Њ—В—Л –≤–Њ –≤—В–Њ—А–Њ–Љ —А–∞—Б—В–≤–Њ—А–µ.
–Э–∞–њ–Њ–Љ–љ–Є–Љ, —З—В–Њ 1 –њ—А–Њ—Ж–µ–љ—В (%) –Њ—В —З–Є—Б–ї–∞ - —Н—В–Њ 0,01 –Њ—В —Н—В–Њ–≥–Њ —З–Є—Б–ї–∞.
–Я–Њ–ї—Г—З–∞–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Ј —Г—Б–ї–Њ–≤–Є—П 1 (–Х—Б–ї–Є –Є—Е —Б–ї–Є—В—М –≤–Љ–µ—Б—В–µ, —В–Њ –њ–Њ–ї—Г—З–Є–Љ —А–∞—Б—В–≤–Њ—А, —Б–Њ–і–µ—А–ґ–∞—Й–Є–є 65% –Ї–Є—Б–ї–Њ—В—Л):
12x+8y=(12+8)*0,65
12x+8y=20*0,65
12x+8y=13
–Я–Њ–ї—Г—З–∞–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Ј —Г—Б–ї–Њ–≤–Є—П 2 (–Х—Б–ї–Є –ґ–µ —Б–ї–Є—В—М —А–∞–≤–љ—Л–µ –Љ–∞—Б—Б—Л —Н—В–Є—Е —А–∞—Б—В–≤–Њ—А–Њ–≤, —В–Њ –њ–Њ–ї—Г—З–µ–љ–љ—Л–є —А–∞—Б—В–≤–Њ—А –±—Г–і–µ—В —Б–Њ–і–µ—А–ґ–∞—В—М 60% –Ї–Є—Б–ї–Њ—В—Л), –і–ї—П —Г–і–Њ–±—Б—В–≤–∞ –≤–Њ–Ј—М–Љ–µ–Љ –њ–Њ –Њ–і–љ–Њ–Љ—Г –Ї–≥ –Ї–∞–ґ–і–Њ–≥–Њ —А–∞—Б—В–≤–Њ—А–∞:
1*x+1*y=(1+1)*0,6
x+y=2*0,6
x+y=1,2
–Я–Њ–ї—Г—З–Є–ї–Є —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є:
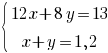
–£–Љ–љ–Њ–ґ–Є–Љ –≤—В–Њ—А–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–∞ 12:
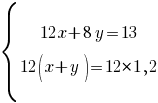
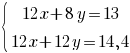
–Р —В–µ–њ–µ—А—М, —З—В–Њ–±—Л –Є–Ј–±–∞–≤–Є—В—М—Б—П –Њ—В "—Е", –≤—Л—З—В–µ–Љ –Є–Ј –≤—В–Њ—А–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –њ–µ—А–≤–Њ–µ:
(12x+12y)-(12x+8y)=14,4-13
12x+12y-12x-8y=1,4
4y=1,4
y=0,35 - —Н—В–Њ –Ї–Њ–љ—Ж–µ–љ—В—А–∞—Ж–Є—П –Ї–Є—Б–ї–Њ—В—Л –≤–Њ –≤—В–Њ—А–Њ–Љ —А–∞—Б—В–≤–Њ—А–µ.
–Э–∞–є–і–µ–Љ, —Б–Ї–Њ–ї—М–Ї–Њ –Ї–Є–ї–Њ–≥—А–∞–Љ–Љ–Њ–≤ –Ї–Є—Б–ї–Њ—В—Л —Б–Њ–і–µ—А–ґ–Є—В—Б—П –≤–Њ –≤—В–Њ—А–Њ–Љ —А–∞—Б—В–≤–Њ—А–µ:
8*0,35=2,8
–Ю—В–≤–µ—В: 2,8
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 AC –Є BD вАУ –і–Є–∞–Љ–µ—В—А—Л –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O. –£–≥–Њ–ї ACB —А–∞–≤–µ–љ 74¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї AOD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
AC –Є BD вАУ –і–Є–∞–Љ–µ—В—А—Л –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O. –£–≥–Њ–ї ACB —А–∞–≤–µ–љ 74¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї AOD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є 15 –Є 3 –њ—А–Њ–≤–µ–і–µ–љ—Л –≤—Л—Б–Њ—В—Л –Ї —Н—В–Є–Љ —Б—В–Њ—А–Њ–љ–∞–Љ. –Т—Л—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і—С–љ–љ–∞—П –Ї –њ–µ—А–≤–Њ–є —Б—В–Њ—А–Њ–љ–µ, —А–∞–≤–љ–∞ 1. –І–µ–Љ—Г —А–∞–≤–љ–∞ –≤—Л—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і—С–љ–љ–∞—П –Ї–Њ –≤—В–Њ—А–Њ–є —Б—В–Њ—А–Њ–љ–µ?
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є 15 –Є 3 –њ—А–Њ–≤–µ–і–µ–љ—Л –≤—Л—Б–Њ—В—Л –Ї —Н—В–Є–Љ —Б—В–Њ—А–Њ–љ–∞–Љ. –Т—Л—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і—С–љ–љ–∞—П –Ї –њ–µ—А–≤–Њ–є —Б—В–Њ—А–Њ–љ–µ, —А–∞–≤–љ–∞ 1. –І–µ–Љ—Г —А–∞–≤–љ–∞ –≤—Л—Б–Њ—В–∞, –њ—А–Њ–≤–µ–і—С–љ–љ–∞—П –Ї–Њ –≤—В–Њ—А–Њ–є —Б—В–Њ—А–Њ–љ–µ?
 –І–µ–ї–Њ–≤–µ–Ї, —А–Њ—Б—В –Ї–Њ—В–Њ—А–Њ–≥–Њ —А–∞–≤–µ–љ 2 –Љ, —Б—В–Њ–Є—В –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 3,5 –Љ –Њ—В —Г–ї–Є—З–љ–Њ–≥–Њ —Д–Њ–љ–∞—А—П. –Я—А–Є —Н—В–Њ–Љ –і–ї–Є–љ–∞ —В–µ–љ–Є —З–µ–ї–Њ–≤–µ–Ї–∞ —А–∞–≤–љ–∞ 1 –Љ. –Ю–њ—А–µ–і–µ–ї–Є—В–µ –≤—Л—Б–Њ—В—Г —Д–Њ–љ–∞—А—П (–≤ –Љ–µ—В—А–∞—Е).
–І–µ–ї–Њ–≤–µ–Ї, —А–Њ—Б—В –Ї–Њ—В–Њ—А–Њ–≥–Њ —А–∞–≤–µ–љ 2 –Љ, —Б—В–Њ–Є—В –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 3,5 –Љ –Њ—В —Г–ї–Є—З–љ–Њ–≥–Њ —Д–Њ–љ–∞—А—П. –Я—А–Є —Н—В–Њ–Љ –і–ї–Є–љ–∞ —В–µ–љ–Є —З–µ–ї–Њ–≤–µ–Ї–∞ —А–∞–≤–љ–∞ 1 –Љ. –Ю–њ—А–µ–і–µ–ї–Є—В–µ –≤—Л—Б–Њ—В—Г —Д–Њ–љ–∞—А—П (–≤ –Љ–µ—В—А–∞—Е).
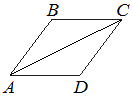 –Т —А–Њ–Љ–±–µ ABCD —Г–≥–Њ–ї ABC —А–∞–≤–µ–љ 146¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ACD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —А–Њ–Љ–±–µ ABCD —Г–≥–Њ–ї ABC —А–∞–≤–µ–љ 146¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ACD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: