Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
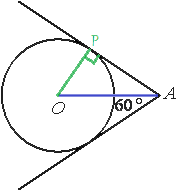Проведем отрезок АО.
Обозначим одну из точек касания окружности и касательной как Р.
Проведем отрезок ОР.
ОР является радиусом и перпендикуляром к касательной АР (по свойству касательной).
Рассмотрим треугольник АОР. Данный треугольник является прямоугольным,т.к. ОР перпендикулярен АР. АО является биссектрисой угла, образованного касательными (свойство касательных прямых).
Следовательно, угол РАО равен половине данного угла, т.е. 30°.
sin∠PAO=sin∠30°=1/2 (табличное значение).
Так же sin∠PAO=ОР/АО (по определению синуса).
sin∠30°=1/2=ОР/АО
AO=2*ОР=2*8=16.
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
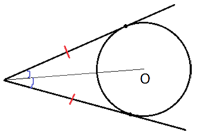
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
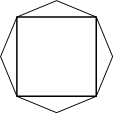Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: