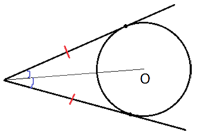
Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
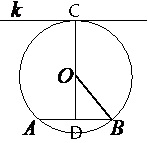Проведем отрезок OB как показано на рисунке.
Расстояние от
хорды AB до параллельной ей
касательной k обозначено как CD.
CD=OC+OD, OC - это радиус окружности, найдем OD.
По условию задачи k||AB. CD перпендикулярен k (по
свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние
накрест-лежащие углы равны), значит треугольник OBD
прямоугольный.
DB=AB/2=40/2=20 (по
второму свойству хорды)
OB равен радиусу окружности.
Тогда по
теореме Пифагора:
OB2=OD2+DB2
292=OD2+202
841=OD2+400
OD2=841-400=441
OD=21
CD=OC+OD=29+21=50
Ответ: 50
Поделитесь решением
Присоединяйтесь к нам...
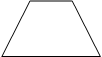Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
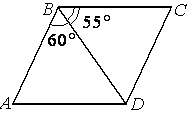Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
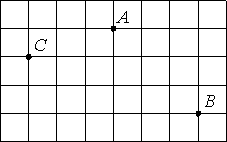На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: