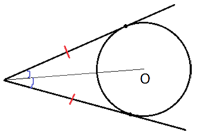
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
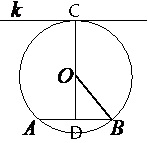Проведем отрезок OB как показано на рисунке.
Расстояние от
хорды AB до параллельной ей
касательной k обозначено как CD.
CD=OC+OD, OC - это радиус окружности, найдем OD.
По условию задачи k||AB. CD перпендикулярен k (по
свойству касательной), тогда CD перпендикулярен и AB (т.к. CD - секущая для параллельных прямых, и внутренние
накрест-лежащие углы равны), значит треугольник OBD
прямоугольный.
DB=AB/2=96/2=48 (по
второму свойству хорды)
OB равен радиусу окружности.
Тогда по
теореме Пифагора:
OB2=OD2+DB2
502=OD2+482
2500=OD2+2304
OD2=2500-2304=196
OD=14
CD=OC+OD=50+14=64
Ответ: 64
Поделитесь решением
Присоединяйтесь к нам...
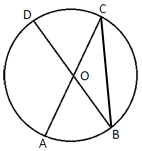В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 128°. Найдите вписанный угол ACB. Ответ дайте в градусах.
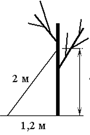Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
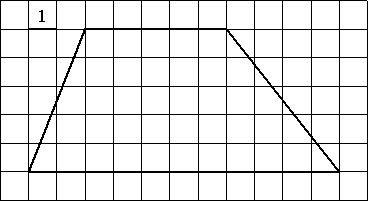Найдите площадь трапеции, изображённой на рисунке.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: