Синус острого угла A треугольника ABC равен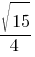 
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться основной тригонометрической формулой:
sin2A+cos2A=1
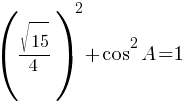
По второму правилу действий со степенями:
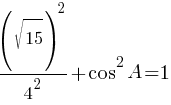
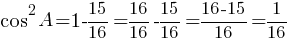
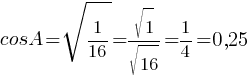
Ответ: 0,25
Поделитесь решением
Присоединяйтесь к нам...
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
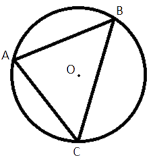Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
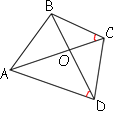В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
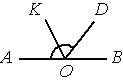Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: