
Косинус острого угла A треугольника ABC равен 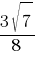 . Найдите sinA.
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
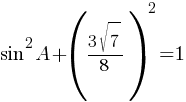

По второму правилу действий со степенями:
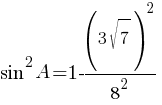
По первому правилу действий со степенями:

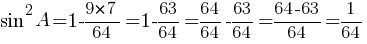
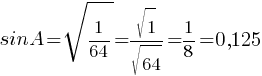 (использовали второе свойство арифметического корня)
(использовали второе свойство арифметического корня)
Ответ: 0,125
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
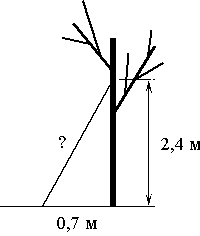 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
Стороны AC, AB, BC треугольника ABC равны 2√
Комментарии: