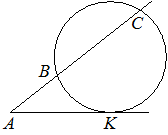
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, BC=32. Найдите AK.
По
теореме о касательной и секущей:
AK2=AB*AC
AK2=4*32=128
AK=√128=√4*32=√4*4*8=√4*4*4*2=
По первому свойству арифметического корня:
=√4*√4*√4*√2=2*2*2*√2=8√2
Ответ: 8√2
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 200√
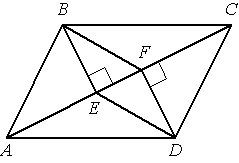В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
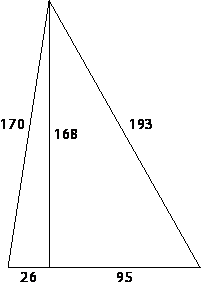Найдите площадь треугольника, изображённого на рисунке.
Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведённую к гипотенузе.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: