Решите уравнение (x-3)2(x-5)=35(x-3).
(x-3)2(x-5)=35(x-3)
(x-3)2(x-5)-35(x-3)=0
Выносим за общую скобку (x-3):
(x-3)((x-3)(x-5)-35)=0
Произведение равно нулю, когда одни из множителей равен нулю, поэтому рассмотрим два случая:
1) x-3=0
x1=3
2) (x-3)(x-5)-35=0
Раскрываем скобки:
x2-5x-3x+15-35=0
x2-8x-20=0
Решим это
квадратное уравнение с помощью
дискриминанта:
D=(-8)2-4*1*(-20)=64+80=144
x2=(-(-8)+12)/(2*1)=(8+12)/2=10
x3=(-(-8)-12)/(2*1)=(8-12)/2=-2
Ответ: x1=3, x2=10, x3=-2
Поделитесь решением
Присоединяйтесь к нам...
После уценки телевизора его новая цена составила 0,99 старой. На сколько процентов уменьшилась цена телевизора в результате уценки?
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 105 человек. Голоса между кандидатами распределились в отношении 2:5. Сколько голосов получил победитель?
Расстояние между пристанями А и В равно 126 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 36 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 105 человек. Голоса между кандидатами распределились в отношении 2:5. Сколько голосов получил победитель?
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Хочу получать новые решения
Ни какого спама
Автор: Таська
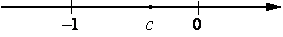
Комментарии: