В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=8.
Рассмотрим треугольник ABF.
По свойству
биссектрисы:
BG/GF=AB/AF=5/3
cosA=AF/AB=3/5 (по
определению косинуса)
Существует тригонометрическая формула:
sin2α+cos2α=1
Тогда:
sin2∠BAF+cos2∠BAF=1
sin2∠BAF+(3/5)2=1
sin2∠BAF=1-9/25
sin2∠BAF=(25-9)/25
sin2∠BAF=16/25
sin∠BAF=4/5
По
теореме синусов:
BC/sin∠BAF=2R
8/(4/5)=8*5/4=10=2R
R=10/2=5
Ответ: 5
Поделитесь решением
Присоединяйтесь к нам...
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Сторона ромба равна 32, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Площадь прямоугольного треугольника равна 968√
Лестница соединяет точки A и B и состоит из 30 ступеней. Высота каждой ступени равна 13 см, а длина – 84 см. Найдите расстояние между точками A и B (в метрах).
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Хочу получать новые решения
Ни какого спама
,
Автор: Таська
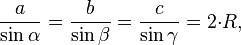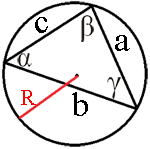
Комментарии: