В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
Вероятность любого события равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
В данной задаче интересующее нас событие - старт спортсмена из России первым.
Старт первым одного из 11-и российских спортсменов - благоприятный исход.
Старт первым одного из 6-и норвежских спортсменов - неблагоприятный исход.
Старт первым одного из 3-х шведских спортсменов - неблагоприятный исход.
Полная группа исходов (благоприятных и неблагоприятных) = 11+6+3=20.
P=11/20=0,55.
Ответ: 0,55
Поделитесь решением
Присоединяйтесь к нам...
В среднем у каждой ученицы класса, где учится Инна, есть по 3 пары сережек. У Инны 5 пар сережек. Какое из следующих утверждений верно?
1) Обязательно есть девочка, у которой вообще нет сережек.
2) Обязательно есть девочка, у которой есть не более двух пар сережек.
3) Обязательно есть девочка, кроме Инны, у которой тоже 5 пар сережек.
4) У всех девочек, кроме Инны, ровно 3 пары сережек.
Стас выбирает трехзначное число. Найдите вероятность того, что оно делится на 48.
В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России.
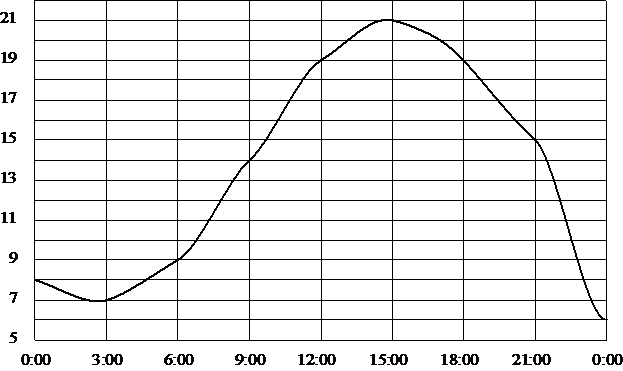На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов в первой половине суток температура не превышала 9°C?
Стрелок 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что стрелок первые 2 раза попал в мишени, а последний раз промахнулся.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: