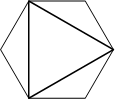
Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
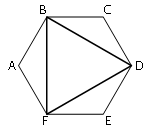Рассмотрим треугольники FAB, BCD и DEF.
Т.к. шестиугольник
правильный, то FA=AB=BC=CD=DE=EF и углы /FAB=/BCD=/DEF. Значит рассматриваемые треугольники равны (по
первому признаку равенства). Следовательно, FB=BD=DF. Т.е. треугольник BDF -
равносторонний.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
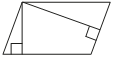Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Площадь прямоугольного треугольника равна 800√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: