
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
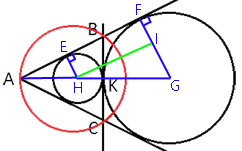 Проведем несколько отрезков:
Проведем несколько отрезков:
EH - радиус малой окружности. Он перпендикулярен AB (по
свойству касательной).
FG - радиус большой окружности. Он перпендикулярен AB (по
свойству касательной).
HG - отрезок, соединяющий центры окружностей и равный R+r, так как он проходит через точку К.
Рассмотрим треугольники AFG и AEH:
∠EAH - общий;
углы AEH и AFG - прямые.
Следовательно эти треугольники
подобны, тогда:
FG/EH=AG/AH
FG/EH=(AH+HG)/AH
32/31=(AH+R+r)/AH
32AH=31(AH+63)
32AH-31AH=1953
AH=1953
sin∠EAH=EH/AH=31/1953=1/63
AK=AH+r=1953+31=1984
AK перпендикулярен BC, т.к. это продолжение большого и малого радиусов, а AB -
касательная (
свойство касательной). AK делит хорду AB пополам (по
свойству хорды).
Треугольник ABC -
равнобедренный, т.к. AK - и
медиана и
высота (
свойство равнобедренного треугольника).
Теперь уберем из рисунка все, что нас больше не интересует и резюмируем, что мы знаем:
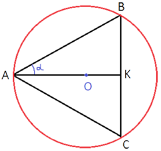 AK=1984
AK=1984
sinα=1/63
Так как AK -
биссектриса, то центр описанной окружности находится на AK.
Найдем AB.
По
теореме Пифагора:
AB2=AK2+BK2
AB2=AK2+(AB*sinα)2
AB2-AB2*sin2α=
19842
AB2(1-1/632)=19842
AB2(632-1)=632*19842
AB2=632*19842/(632-1)
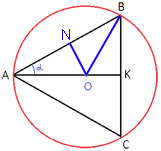 Рассмотрим треугольник AOB.
Рассмотрим треугольник AOB.
AO=OB, так как это радиусы окружности, следовательно данный треугольник
равнобедренный.
Проведем высоту ON, в
равнобедренном треугольнике она так же является и
медианой (по
свойству равнобедренного треугольника).
sinα=ON/AO => ON=AO/63
По теореме
Пифагора:
AO2=ON2+AN2
AO2=AO2/632+(AB/2)2
AO2-AO2/632=AB2/4
AO2(1-1/632)=AB2/4
AO2((632-1)/632)=(632*19842/(632-1))/4
4AO2=632*19842/(632-1)/((632-1)/632)=632*19842*632/(632-1)2
2AO=632*1984/(632-1)
2AO=3969*1984/3968=3969/2=1984,5
AO=992,25
Ответ: 992,25
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
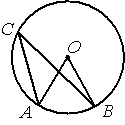 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
 Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
 Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.

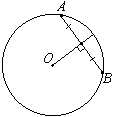
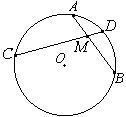
Комментарии:
(2017-03-21 19:51:48) Администратор: Мария, конечно это опечатка, спасибо большое, что заметили. Исправлено.
(2017-03-19 18:42:33) Мария: АК не может быть перпендикулярен АВ!!! может быть ВС?