Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
По свойству
равнобедренной трапеции - углы при основании равны.
Тогда ∠ADC=∠BAD=30°+45°=75°.
Сумма углов четырехугольника равна 360°, тогда получаем, что:
360°=75°+75°+∠DCB+∠CBA,
∠DCB+∠CBA=360°-75°-75°=210°, а учитывая, что ∠DCB=∠CBA (по тому
свойству равнобедренной трапеции), получаем ∠DCB=∠CBA=210°/2=105°, эти углы и есть бОльшие в трапеции
Ответ: 105
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
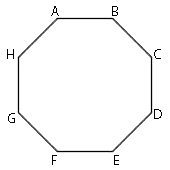ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: