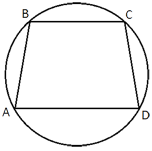Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Описать окружность можно только около
равнобокой трапеции (по
свойству трапеции).
Получается, что наша
трапеция - равнобокая (или равнобедренная).
Пусть 49° равняется угол BAD.
∠BAD=∠ADC=49° (по
свойству равнобедренной трапеции).
Сумма углов выпуклого n-угольника вычисляется по формуле (n-2)180°, тогда сумма углов трапеции равна (4-2)180°=360°.
360°=∠BAD+∠ADC+∠DCB+∠CBA
360°=49°+49°+∠DCB+∠CBA
∠DCB+∠CBA=262°
∠DCB=∠CBA (по
свойству равнобедренной трапеции).
Тогда ∠DCB=∠CBA=262°/2=131°
Ответ: ∠DCB=∠CBA=131°, ∠BAD=∠ADC=49°
Поделитесь решением
Присоединяйтесь к нам...
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
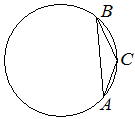В треугольнике ABC угол C равен 135°, AB=14√2. Найдите радиус окружности, описанной около этого треугольника.
Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-16 19:27:30) Светлана: Пусть угол А равен 39 гр. Углы А и В внутренние односторонние при параллельных BC и АD и секущей AB. Тогда угол B равен 180-39 = 141. Условие вписанного в окружность четырёхугольника: сумма противоположных углов равна 180 градусов. Значит угол С равен 180-39 = 141. Тогда на угол D приходится 39 градусов.
(2015-05-05 12:17:53) Жека: АВТАР ВАЩЕ КРАСАВА