В трапеции ABCD AB=CD, ∠BDA=67° и ∠BDC=28°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=67°+28°=95°
Т.к. AB=CD, то
трапеция ABCD -
равнобедренная.
Тогда ∠ADC=∠BAD=95° (по
свойству равнобедренной трапеции).
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ADB+∠ABD
180°=95°+67°+∠ABD
∠ABD=18°
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
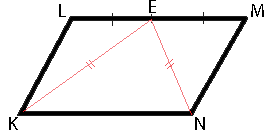В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
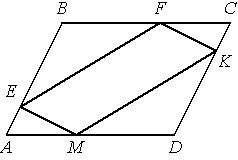В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: