
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ261 –ł–∑ 1087 |
 –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABC —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD, –Ķ—Ā–Ľ–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ AD –ł –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ CD —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ 30¬į –ł 80¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ.
–Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABC —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD, –Ķ—Ā–Ľ–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ AD –ł –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ CD —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ 30¬į –ł 80¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ.
–£–≥–ĺ–Ľ ∠BCA=∠CAD, —ā.–ļ. —ć—ā–ĺ
–≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ł–Ķ –Ĺ–į–ļ—Ä–Ķ—Ā—ā-–Ľ–Ķ–∂–į—Č–ł–Ķ —É–≥–Ľ—č.
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, ∠BCD=80¬į+30¬į=110¬į.
–ü–ĺ
—Ā–≤–ĺ–Ļ—Ā—ā–≤—É —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ∠BCD=∠ABC=110¬į.
–ě—ā–≤–Ķ—ā: ∠ABC=110¬į
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ –≤–Ķ—Ä—ą–ł–Ĺ—É C –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ —ā–ĺ—á–ļ–Ķ B. –Ě–į–Ļ–ī–ł—ā–Ķ AC, –Ķ—Ā–Ľ–ł –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 7.5, –į AB=2.
–ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ AC —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ –≤–Ķ—Ä—ą–ł–Ĺ—É C –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AB –≤ —ā–ĺ—á–ļ–Ķ B. –Ě–į–Ļ–ī–ł—ā–Ķ AC, –Ķ—Ā–Ľ–ł –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ 7.5, –į AB=2.
 –Ě–į–Ļ–ī–ł—ā–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD, –Ķ—Ā–Ľ–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ AD –ł –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ AB —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ 46¬į –ł 35¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–Ě–į–Ļ–ī–ł—ā–Ķ –Ī–ĺ–Ľ—Ć—ą–ł–Ļ —É–≥–ĺ–Ľ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD, –Ķ—Ā–Ľ–ł –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ AD –ł –Ī–ĺ–ļ–ĺ–≤–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–ĺ–Ļ AB —É–≥–Ľ—č, —Ä–į–≤–Ĺ—č–Ķ 46¬į –ł 35¬į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –•–ĺ—Ä–ī—č AC –ł BD –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ P, BP=7, CP=14, DP=10. –Ě–į–Ļ–ī–ł—ā–Ķ AP.
–•–ĺ—Ä–ī—č AC –ł BD –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –≤ —ā–ĺ—á–ļ–Ķ P, BP=7, CP=14, DP=10. –Ě–į–Ļ–ī–ł—ā–Ķ AP.
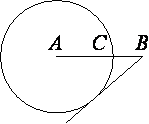 –Ě–į –ĺ—ā—Ä–Ķ–∑–ļ–Ķ AB –≤—č–Ī—Ä–į–Ĺ–į —ā–ĺ—á–ļ–į C —ā–į–ļ, —á—ā–ĺ AC=75 –ł BC=10. –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ A, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ C. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ł–∑ —ā–ĺ—á–ļ–ł B –ļ —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–Ě–į –ĺ—ā—Ä–Ķ–∑–ļ–Ķ AB –≤—č–Ī—Ä–į–Ĺ–į —ā–ĺ—á–ļ–į C —ā–į–ļ, —á—ā–ĺ AC=75 –ł BC=10. –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ A, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ C. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ł–∑ —ā–ĺ—á–ļ–ł B –ļ —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–ö–į–ļ–ł–Ķ –ł–∑ –ī–į–Ĺ–Ĺ—č—Ö —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ –≤–Ķ—Ä–Ĺ—č? –ó–į–Ņ–ł—ą–ł—ā–Ķ –ł—Ö –Ĺ–ĺ–ľ–Ķ—Ä–į.
1) –ē—Ā–Ľ–ł —ā—Ä–ł —É–≥–Ľ–į –ĺ–ī–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č —ā—Ä—Ď–ľ —É–≥–Ľ–į–ľ –ī—Ä—É–≥–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–ĺ —ā–į–ļ–ł–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
2) –í –Ľ—é–Ī–ĺ–ľ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł –≤–∑–į–ł–ľ–Ĺ–ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č.
3) –£ —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ķ—Ā—ā—Ć —Ü–Ķ–Ĺ—ā—Ä —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł.
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2021-10-04 12:42:21) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –ü–ĺ—ā–ĺ–ľ—É, —á—ā–ĺ AB –Ĺ–Ķ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į CD.
(2021-09-30 09:52:25) : –į –Ņ–ĺ—á–Ķ–ľ—É —É–≥–Ľ–į BAC –ł ACD –Ĺ–Ķ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –Ĺ–į–ļ—Ä–Ķ—Ā—ā –Ľ–Ķ–∂–į—Č–ł–ľ–ł?