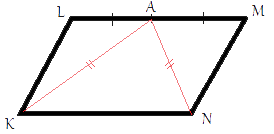
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники KLA и NMA. LA=MA, т.к. точка А - середина LM, AK=AN из условия задачи, LK=MN (по свойству параллелограмма). Соответственно, треугольники KLA и NMA равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что ∠KLA=∠NMA.
LK||MN (по определению параллелограмма), рассмотрим сторону LM как секущую к этим параллельным сторонам. Тогда получается, что сумма углов KLA и NMA равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.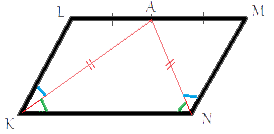
Рассмотрим треугольник KAN, KA=NA (по условию задачи), соответственно, этот треугольник
равнобедренный. Отсюда следует, что ∠AKN=∠ANK (
из свойства равнобедренного треугольника). Из ранее полученного равенства треугольников, следует, что ∠LKA=∠MNA. Получаем, что углы LKN и MNK равны.
В свою очередь они так же являются внутренними односторонними и их сумма равна 180°. Получается, что и эти углы равны 90° каждый.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
Центральный угол AOB равен
60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 12 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 9 м. Найдите длину троса.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: