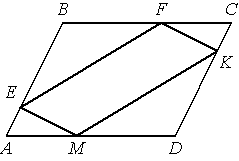
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
1) Рассмотрим треугольники EBF и KDM.
BF=DM (по условию задачи)
/B=/D (по
свойству параллелограмма)
BE=DK (по условию задачи).
Следовательно, треугольники EBF и KDM равны (по первому признаку).
Поэтому ЕF=KM.
2) Рассмотрим треугольники AEM и FCK.
Т.к. AB=CD и AD=BC (по
свойству параллелограмма), а BF=DM и BE=DK (по условию задачи), то AE=CK и AM=CF.
/A=/C (по
свойству параллелограмма).
Следовательно, треугольники AEM и FCK (по первому признаку). А это значит, что EM=FK.
Из пунктов 1 и 2 (равенство сторон) следует, что EFKM —
параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
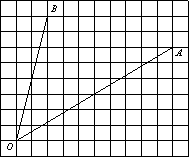Найдите тангенс угла AOB.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Радиус окружности, описанной около равностороннего треугольника, равен 12. Найдите высоту этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: