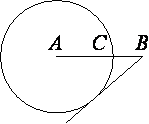На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
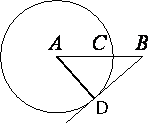Проведем отрезок AD, где D - точка касания
окружности и
касательной.
AD перпендикулярен к
касательной (по
свойству касательной), т.е. угол между AD и
касательной DB равен 90°.
Следовательно, треугольник ABD -
прямоугольный.
AD=AC=75 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По
теореме Пифагора: AB2=AD2+BD2
(75+10)2=752+BD2
7225=5625+BD2
BD2=1600
BD=40
Ответ: длина касательной равна 40.
Поделитесь решением
Присоединяйтесь к нам...
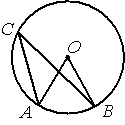Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Площадь прямоугольного треугольника равна 18√
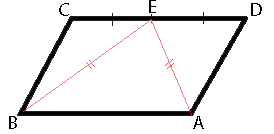В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
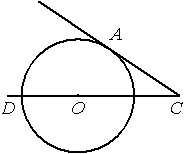Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: