
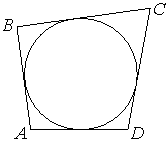
 Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
По
свойству вписанной в четырехугольник окружности:
AD+BC=AB+CD
AD+13=9+18
AD=9+18-13=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
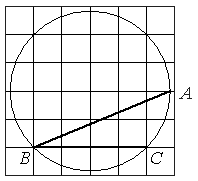 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
 Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=11, AD=15, AC=52. Найдите AO.
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
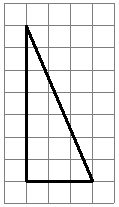 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
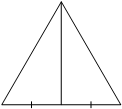 Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
 («простой»), должен быть выпуклым.
(«простой»), должен быть выпуклым.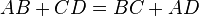
Комментарии: